Le tempérament en musique
Il y a évidemment une infinités d’intervalles possibles dans une musique : la sirène nous les fait entendre théoriquement tous... mais s’agissant de les choisir et les mesurer, chaque civilisation a établi différentes échelles et systèmes pour y parvenir ; un mode, une gamme, un accord sont définis par les intervalles existants entre leurs sons consécutifs. Depuis Pythagore, les intervalles ont été déterminés de plusieurs manières en occident, ce qui a donné naissance à différents systèmes musicaux voisins... Lire la suite
SOMMAIRE
La délicate question de l’évaluation d’un intervalle
L’émergence des instruments à sons fixes
Appreciation de la justesse : nature ou culture ?
Des tempéraments nécessaires
La révolution du tempérament égal
La délicate question de l’évaluation d’un intervalle
Il y a évidemment une infinités d’intervalles possibles dans une musique : la sirène nous les fait entendre théoriquement tous... mais s’agissant de les choisir et les mesurer, chaque civilisation a établi différentes échelles et systèmes pour y parvenir ; un mode, une gamme, un accord sont définis par les intervalles existants entre leurs sons consécutifs. Depuis Pythagore, les intervalles ont été déterminés de plusieurs manières en occident, ce qui a donné naissance à différents systèmes musicaux voisins :
Par le "cycle des quintes" : la gamme pythagoricienne
Comme nous l’avons expliqué dans nos tous premiers cours (cédérom 1), Pythagore nous a livré la justification scientifique des 7 notes qui composent notre gamme diatonique : il a découvert en effet qu’en partageant une corde tendue, le célèbre et légendaire monocorde, en 2 parties égales, chacune des deux parties émet une note située à l’octave supérieure de la note donnée par la corde vibrant sur toute sa longueur et qu’en plaçant le chevalet au tiers de cette corde ; on obtient cette fois-ci la quinte de la corde à vide. Il a alors montré qu’il est possible à l’aide de ces deux seuls intervalles d’octaves et de quinte de reconstituer l’échelle musicale toute entière : c’est ce qu’on appelle maintenant le "cycle des quintes", sorte d’archétype musical permettant de justifier la place de chaque note en la fixant avec précision : à chaque fois que l’on élève une note d’une quinte, on multiplie sa fréquence par 3/2 ; si on l’abaisse d’une quinte, on multiplie par 2/3. La gamme engendrée par ce système est souvent appelée "gamme des violonistes", car la tierce majeure y est plus haute que dans notre gamme diatonique usuelle, et la tierce mineure plus basse. Pourquoi cette appellation ? parce que les instruments à sons non fixes, comme les cordes, incitent à jouer d’oreille la tierce plus grande (attraction vers la quarte) ; tout comme à jouer plus haut les notes diésées et plus bas les notes bémolisées (do# plus haut que réb). Ainsi Arnolt Schlick (1460 1521 : organiste et compositeur allemand) recommande déjà aux harpistes et à tous les instruments à cordes de s’accorder par quintes ascendantes jusqu’à do# et par quinte descendantes jusqu’à lab. Cette méthode donne un excellent résultat sonore, très favorable aux modulations.
Par la série des harmoniques : la gamme zarlinienne
L’acoustique montre qu’un son musical n’est jamais "simple", il contient toujours un son fondamental, correspondant à la note la plus grave que peut émettre la corde, et des sons "partiels" ou "concomitants", qui sont des facteurs déterminants de son timbre : ce sont ses harmoniques.
De nombreuses expériences simples permettent de mettre en évidence les harmoniques. En voici deux exemples :
1) Chanter "ou" sur cette note :
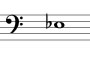
puis jouer doucement sur le piano et laisser mourir le son en chantant toujours :
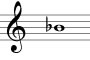
On continuera d’entendre dans la voix, mêlé au mib fondamental, le 3ème harmonique sib.
2) Sur un clavier de piano, enfoncer successivement dans les faire jouer les touches correspondant au deux notes :
En même temps, attaquer sèchement de l’autre main cette note sans la tenir :
Les cordes correspondant au fa et au lab graves, résonneront partiellement en reproduisant avec un timbre très pur, le do supérieur, leur harmonique commun. (Ce fa et ce lab sont appellés "harmoniques inférieurs" de do.)
La fréquence de ces sons harmoniques est un multiple simple de la fondamentale F ; 2F ; 3F ;.etc...
La série des harmoniques naturels de chaque son donne tous les intervalles pouvant être exprimés par des fractions, puisque le nombre désignant le rang de chaque harmonique est proportionnel à la fréquence. On trouve notamment les intervalles d’octave (2/1), de quinte (3/2), de quarte (4/3), de tierce majeure (5/4) et mineure (6/5)... Le "système de Zarlino" (et de plusieurs théoriciens arabes) dérive de cette méthode. L’accord parfait nous est donné par les harmoniques de rangs 4, 5 et 6 d’une note quelconque. Pour le do par exemple, ce sera do, mi, et sol. La gamme est elle-même le résultat de 3 accords parfaits naturels dit "générateurs" , l’un placé sur la tonique do et les deux autres sur les notes qui se trouvent à une distance de quinte juste -naturelle- de cette tonique, l’une à la quinte supérieure sol, l’autre à la quinte inférieure fa : fa-la-do ; do-mi-sol ;sol-si ré. On peut donc présenter la gamme de Zarlino comme résultant de l’enchaînement de 3 quintes naturelles fa-do-sol-ré, chaque quinte étant meublée par une note formant tierce naturelle avec la note grave de la quinte (1). Pour obtenir la gamme de do majeur il suffit alors de ramener les notes obtenues à l’intérieur d’une octave allant d’un do à un autre do (2) Rameau obtient les principaux intervalles du système de Zarlino en posant seulement les 5 premiers harmoniques, puis les 5 premiers harmoniques de chacun d’entre eux, et ainsi de suite.
A écouter : RAVEL :"Ma mère l’Oye, (II "le Petit Poucet" : imitation d’un chant d’oiseau par des glissandos de violon en harmonique). Concerto pour piano en sol (1er mouvment : harmoniques de harpe (thème) accompagnés de glissandos). Musique Tzigane, nombreux exempkes. - BARTÓK : Danses roumaines (n°3), version pour violon entièrement en harmonique.
Plusieurs autres méthodes d’évaluation des intervalles ont été élaborés ; pour autant toutes les gammes (à l’exception de la gamme de Zarlino) reposent sur le fameux cycle des quintes, tant cet intervalle est dans notre musique la mesure de toute chose. Mais cependant, quelque soit le système adopté, les instrumentistes sont toujours confrontés à un même dilemme : une note peut avoir différentes valeurs, certes très voisines, selon le système utilisé. Par exemple :
> le MI obtenu par 4 quintes successives à partir du DO est supérieur d’un comma au MI 5ème harmonique du même Do.
> Trois tierces majeures forment un intervalle (do-si#) inférieur à l’octave d’une diésis (petit quart de ton) ou supérieur d’un comma pythagoricien selon le type de tierce majeure considéré (mi haut ou mi bas).
>Douze quintes successives à partir de do donnent encore un SI# supérieur d’un comma pythagoricien à la 7ème octave de do (nous avons là deux SI # différents, tous deux différents de do !!).
L’émergence des instruments à sons fixes
Le chanteur et le violoniste n’ont pas à s’occuper de ces subtilités : ils donneront naturellement l’intervalle juste en fonction du contexte : libres de leur fréquence, ils peuvent émettre une infinité de sons de hauteur différentes à l’intérieur d’une octave. Mais tous les instrumentistes n’en diront pas autant.
Dès le XIVème, la prépondérance bientôt tyrannique du mode de do (notre gamme diatonique majeure) due sans doute à sa remarquable symétrie (do-ré-mi-fa -> 1 ton-1ton-1/2 ton : sol-la-si-do ->1 ton-1ton-1/2 ton) ouvre la voie à la modulation, dans le sens moderne du mot par imitation à la quinte. De plus, la polyphonie se développant, les altérations sont beaucoup plus utilisées (cf nos précédents articles l’évolution du contrepoint). Il devient difficile aux instruments à son fixe (toute sorte d’instruments à clavier ou à trous) qui ne peuvent fournir qu’un nombre limité de son par octave, d’être accordés correctement, et de sonner juste en toute circonstances, dans toutes les tonalités, et tous les modes, et qui puis est dans des situations d’accompagnement, sans parler ensuite des instruments transpositeurs.
Il devient nécessaire d’éliminer autant que possible l’effet sensible des commas, en plaçant ou en répartissant ceux-ci dans des intervalles inusités, l’enjeu étant d’approcher au plus près la pureté des principaux intervalles ; en l’occurrence les octaves et les quintes : mais alors, ce sont les tierces qui ne sonnent plus juste ! Sans parler des difficultés insurmontables que posent aux facteurs d’instruments d’alors, les notes enharmoniques, c’est à dire les notes différentes produisant le même son à l’oreille : do#, reb ; ré# mib etc... car enfin un violoniste ne joue pas toujours un do# comme un réb. Il ne jouera pas non plus un do#, 5ème degré du ton de fa# comme un do# 7ème degré du ton de ré ; dans ce dernier cas, l’attraction de la tonique ré l’amenant souvent à jouer un do # sensiblement plus haut. Pour qu’une telle chose soit possible sur un clavier, il aurait fallut par octave trois fois plus de touches qu’il n’y a de notes dans la gamme diatonique, soit 3x7=21 touches par octave....
Appreciation de la justesse : nature ou culture ?
La différence de ces minuscules commas (1/9ème de ton) produit néanmoins sur l’oreille des effets indubitables [1] : ils peuvent transformer n’importe quelle musique, aussi parfaite soit-elle, en une cacophonie criarde, nous donner la désagréable impression d’un morceau mal joué, maladroit, écrit par un sourd et interprété par un débutant ! Nous découvrons là le corolaire de tout système musical : la justesse, c’est à dire la formalisation conjointe de notre pensée et notre oreille musicale.
Nous pouvons même aller plus loin, en considérant la conception zarlinienne d’un intervalle "juste" : ayant établi sa gamme selon les lois de la résonance, Zarlino affirme qu’un intervalle est juste s’il est naturel, c’est à dire composé d’un son et la série de ses harmoniques naturelles ; un tel intervalle ayant pour caractéristique essentielle de ne produire aucun battement [2] en émission harmonique (accord plaqué). L’ordonnance et la simplification merveilleuse des rapports de fréquence obtenus a séduit nombre de mathématiciens et philosophes de la Renaissance. "Malheureusement, cette perfection formelle n’existe que sur le papier, car l’audition de musique interprétée dans cette gamme nous révèle "l’imposture d’une conception qui n’a de naturel que le nom et que ne peut que rejeter tout musicien non atteint de surdité musicale !" affirme Serge Cordier, imminent accordeur, musicologue, et inventeur du tempérament égal à quintes justes (cf liens complémentaires).
Il poursuit : "Sans toujours nier le rôle de la résonance, qui est à la source des conceptions pythagoriciennes et zarliniennes, de nombreux musicologues laissent entendre que la conception de la justesse n’a cessé d’évoluer en fonction des transformations successive du langage musical et que, par conséquent, la gamme serait tout autant , et peut-être même davantage, un fait de culture qu’un fait de nature. Dans cette perspective, on considère généralement, que la justesse aurait été pythagoricienne au temps de la monodie et des débuts de la polyphonie jusqu’au XVème siècle environ (polyphonie contrapuntique) puis le sentiment de la justesse se serait transformé et serait devenu zarlinien avec l’apparition de la consonance de tierce, et la prise de conscience de la dimension verticale de la musique (naissance de la notion d’accord, de l’accord parfait, du style harmonique et de la mélodie accompagnée du XVIIIe au XVIII e environ). Cette conception à dominante zarlinienne aurait prévalu jusqu’à J.S. Bach"
Des tempéraments nécessaires
Pour éliminer autant que possible l’effet sensible des commas, il a fallut "tempérer" : c’est à dire trouver des compromis pour pouvoir diviser l’octave en un certain nombre de parties égales ou inégales : le mot "tempérament" ne s’appliquant pas comme on le croit trop souvent à la gamme bien tempérée traditionnelle. Tempéraments inégaux, tempéraments mésotoniques, tempéraments par division multiples... Le nombre de tempéraments qui ont été inventés pendant la Renaissance et la période baroque est considérable ; Christian Huygens (1629-1695 à La Haye), Hollandais de Paris, est partisan d’une division théorique de l’octave en 31 intervalles. Holder lui, divise théoriquement l’octave en 53 neuvième de ton...
Les tempéraments sont devenus nécessaires au fur et à mesure du développement de la musique, parce qu’aucune gamme théorique n’est utilisable en pratique : elles incluent toutes au moins un intervalle désagréable, sonnant faux ; seul le tempérament , qui ne le rend pas pour autant juste, peut le rendre praticable. Un compromis devient nécessaire entre justesse de certains intervalles, fausseté pas trop marquée des autres, possibilités de transposition et/ou de modulation.
Le cœur du problème est posé : comment rendre les vingt quatre tons vraiment utilisables dans la pratique ? À propos du clavecin et du clavicorde, Carl Philippe Emmanuel Bach (deuxième fils survivant de Jean-Sébastien Bach, né à Weimar le 8 mars 1714 et mort à Hambourg le 14 décembre 1788 ) écrit : « Les deux sortes d’instruments doivent être bien tempérés : en accordant les quartes et les quintes, avec les tierces majeures et mineures et les accords complets pour preuves, il faut affaiblir un tant soit peu la justesse des quintes, en sorte que l’oreille la perçoive à peine et que les vingt quatre tons soient tous utilisables. »
La révolution du tempérament égal
Dès le XVIe, et au XVIIe avec Werckmeister (né en 1645 et mort à Halberstadt en 1706 ) et l’apparition du piano forte, se généralise la division de l’octave en douze 1/2 tons tous égaux, ce qui permet de confondre les notes enharmoniques. Ce tempérament égal (ou gamme tempérée ; appellation contestable car toutes les gammes aux tempérament inégaux sont tempérées) consiste à réduire les quintes de 1/12e de comma pythagoricien. Les quintes raccourcies , l’octave sonne parfaitement. Cette idée simple permet toutes les transpositions et toutes les modulations imaginables, puisque toutes les notes sont équivalentes quand on les considère comme toniques. On arrive enfin à la liberté recherchée : on peut maintenant aborder tous les tons majeurs et mineurs sans en privilégier certains au détriment d’autres. C’est pourquoi ce même tempérament sera bien des siècles plus tard la condition même du système dodécaphonique sériel, qui ne supporte justement aucune polarisation tonale. La gamme tempérée égale est en effet purement une série (une série de notes homogenement réparties, mais dépourvues de consonances communes ), et non le résultat d’une construction harmonique telle que le sont les autres systèmes.
Il faut reconnaitre pourtant que cette solution n’est idéale ... que pour le profane. En revanche, pour le musicien contemporain de l’adoption de ce nouveau tempérament, tous les intervalles sont légèrement faux à l’exception des octaves. Tous les accords sont dénaturés, notamment l’accord parfait avec sa tierce corrompue ; et les consonances perdent leur caractères spécifiques par l’apparition de battements entre les harmoniques communs dont l’unisson est imparfait. Mais surtout les tonalités ont perdu leur "couleur", couleurs qui importaient beaucoup aux oreilles affinées comme celles d’un Mozart ou même d’un Rameau qui redoutait cet inconvénient, même s’il en défendait le principe. La modulation devient une transposition stricte. Une fois installé dans la nouvelle tonalité, l’effet de surprise passé, tout se passe comme si on avait changé de diapason ; le sentiment, la "couleur", elle, ne change pas.
L’habitude aidant, puisque de nos jours quasiment toutes les musiques que nous entendons l’utilisent, les inconvénients pourtant notables du tempérament égal ne choquent personne, et c’est au contraire les anciens tempéraments qui surprennent notre oreille lorsque nous les expérimentons pour la première fois. Le violoncelliste et chef d’orchestre Nikolaus Harnoncourt va jusqu’à écrire : "Moi-même je suis tellement habitué aux tempéraments inégaux que le piano tel qu’on l’entend habituellement me paraît effroyablement faux, même s’il est très bien accordé". Le tempérament égal est de nos jours utilisé de façon presque universelle dans la musique occidentale [3].
"Par son admirable Wohltemperierte Klavier, J.S. Bach propose une série de pièces dans toutes les tonalités majeures et mineures, que seul un "clavier bien tempéré" permet de jouer de façon satisfaisante. Pour autant, cela ne prouve pas que Bach ait préconisé un tempérament égal. Faut-il en effet que toutes les gammes soient rigoureusement identiques comme les théoriciens l’ont cru nécessaire ? N’est-il pas suffisant qu’elles soient analogues ?... L’échelle cyclique formé par la méthode de Schlick , ou mieux en prenant les six premières quintes ascendantes et les cinq premières quintes descendantes, offre une excellente solution au tempérament, très favorable aux modulations [...] comme celui de Serge Cordier qui conserve les quintes justes et augmente les octaves de 1/7e de comma.". Nous resterons pour conclure avec Roland de Candé sur cette épineuse question...
Sources & liens complémentaires
Serge CORDIER : Piano bien tempéré et justesse orchestrale (ed Bucher/Chaste 1982). Voir son site : Le tempérament Cordier
Roland de CANDÉ : Nouveau dictionnaire de la musique (ed Seuil 1986)
Musique et tempéraments sur le site très complet de Didier Guiraud de Willot "L’orgue à nos logis"
http://pagesperso-orange.fr/organ-au-logis/Pages/Temperam.htm#DatesEgal
Sur Wikipédia :
Notes
[1] Le pouvoir discriminateur est, rappelons-le, de l’ordre du savart, soit 1/50 de ton en justesse mélodique, c’est à dire lorsque 2 sons sont entendus l’un après l’autre, et nettement inférieur au savart en justesse harmonique, c’est à dire lorsque 2 sons sont perçus simultanément : il peut alors atteindre le cent : soit 1/200ème de ton.
[2] Si 2 sons de fréquences voisines N2 et N1 sont entendus simultanément, on perçoit alors des battements, c’est à dire des variations périodiques de l’intensité. Les battements entre sons fondamentaux ne doivent pas exister sur un piano bien accordé : ils caractérisent en effet un unisson défectueux où les 3 cordes d’une même note ne sont pas exactement à la même hauteur.
[3] A noter, cependant, que le piano sort de l’échelle du tempérament égal dans l’aigu, sans quoi il sonnerai faux : le son de ses cordes aiguës étant trop pauvre en harmoniques, et donc sonnant naturellement trop bas.
